温馨提示:本文过于抽象,慎入。
我们都知道,对于计算机来说,与外界交互的流程大概是输入 => 处理 => 输出。不妨试试将目光拉长,世界上的种种事物都符合这样的抽象模型。再拓展看看,我们的世界也能进行这样的抽象。
本篇文章,主要用于来开开脑洞。
# 单体模型
# 个体
世上万物,皆是相互依赖而生。拿我们人类来说,既是独立的个体,同时也免不了与其他人或事物的交流。我们听到的、看到的、感受到的、触摸到的,经过复杂的神经传递、处理,然后反馈到身体的各个部位,再分别作出反馈。
上面这一段,我们来分析看看:
function 人体(听觉, 视觉, 触觉, ...其他感觉) {
传递(听觉, 视觉, 触觉, ...其他感觉);
反馈 = 处理(听觉, 视觉, 触觉, ...其他感觉);
return 反馈;
}
我们来抽象一下:
function 个体(输入) {
输出 = 处理(输入);
return 输出;
}
我们仔细观察,可以发现这个模型适用于任何事物,当然至于事物存在的主观性和客观性哲学问题这里暂不讨论。
# 群体
在这里,群体依然可以抽象为个体。
# 1. 宏观角度
宏观上看,我们可以忽略个体之间的影响,或者说个体之间的影响并不能影响整体,我们可以得到:
群体 = 个体;
此时我们可以知道,群体符合上方所述的个体模型。
# 2. 微观角度
微观上看,群体由多个个体组成,其中也包括了个体间的相互作用:
群体 = 个体 + ... + 个体 + 各个个体间的相互作用
// 1. 假设个体间满足串行关系
function 群体(输入){
个体1输出 = 个体1处理(输入);
个体2输出 = 个体2处理(个体1输出);
...
个体n输出 = 个体n处理(个体n-1输出);
return 个体n输出;
}
// 2. 假设个体间满足并行关系
function 群体(输入){
// 拆分给各个个体的输入,分别处理
for(var i = 0; i < 个体.length; i++){
个体i输入 = 获取个体输入(输入, i);
个体i输出 = 个体i处理(个体i输入)
}
// 汇总输出
总输出 = 汇总([...各个个体的输出]);
return 总输出;
}
不管群体中个体间是并行、串行关系,还是其他更加复杂的关系,最后我们总会发现,微观角度的群体也总能满足个体模型,我们将其称作“单体模型”:
// 单体模型
function 单体(输入) {
输出 = 处理(输入);
return 输出;
}
# 交互
前面也说了,作为独立的个体,同时个体与个体之间也存在交流,可以理解为交互。 我们抽象完单体,现在来看看单体间的交互(交流),首先我们从人机交互开始。
# 人机交互
作为一个程序员,一天几乎有一半时间都在电脑面前,我们将人和电脑的互动归类为“人机交互”。
简单来说,人机交互无非包括两个过程:
- 人 => 机:通过操作对机器进行输入,例如从键盘输入内容、用鼠标点击某些元素等
- 机 => 人:机器拿到输入内容,根据程序进行计算,可通过显示器、声音设备进行输出
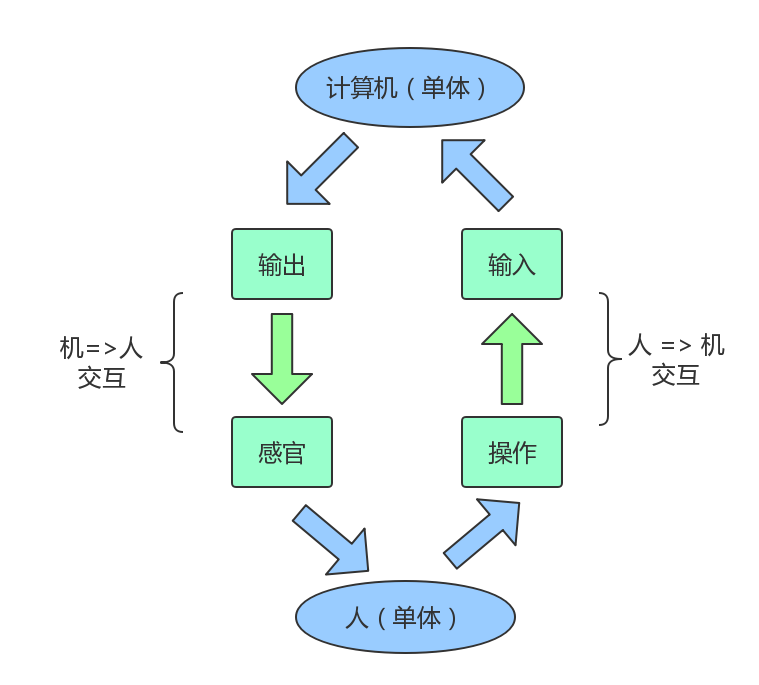
以上的过程我们可以抽象为两两单体之间的交互:
function 人(输入) {
输出 = 处理(输入);
return 输出;
}
function 机(输入) {
输出 = 处理(输入);
return 输出;
}
// 1. 输入从机开始
人的输入 = 机(输入);
机的输入 = 人(人的输入);
// 2. 输入从人开始
机的输入 = 人(输入);
人的输入 = 机(机的输入);
我们得到一个鸡生蛋蛋生鸡的模型。
# 多体交互
多体交互比两体交互稍微复杂,因为每个单体接收的输入是所有其他单体汇总的输入,而每个单体提供的输出也将成为所有其他单体输入直接或间接的影响。
这段话是不是有些似曾相识,因为它部分符合我们在前面讨论的微观群体的模型,也就是说我们在群体中:
const 单体1输入 = 汇总(...其他n-1个单体的输出);
我们发现,汇总这个处理,与单体的模型非常相似,我们将其定义为一种交互介质:
function 交互介质(单体输出) {
单体输入 = 处理(单体输出);
return 单体输入;
}
这个模型与单体模型完全一致,也就是说,交互介质也是单体的一种,这时候我们人机交互过程图调整为:
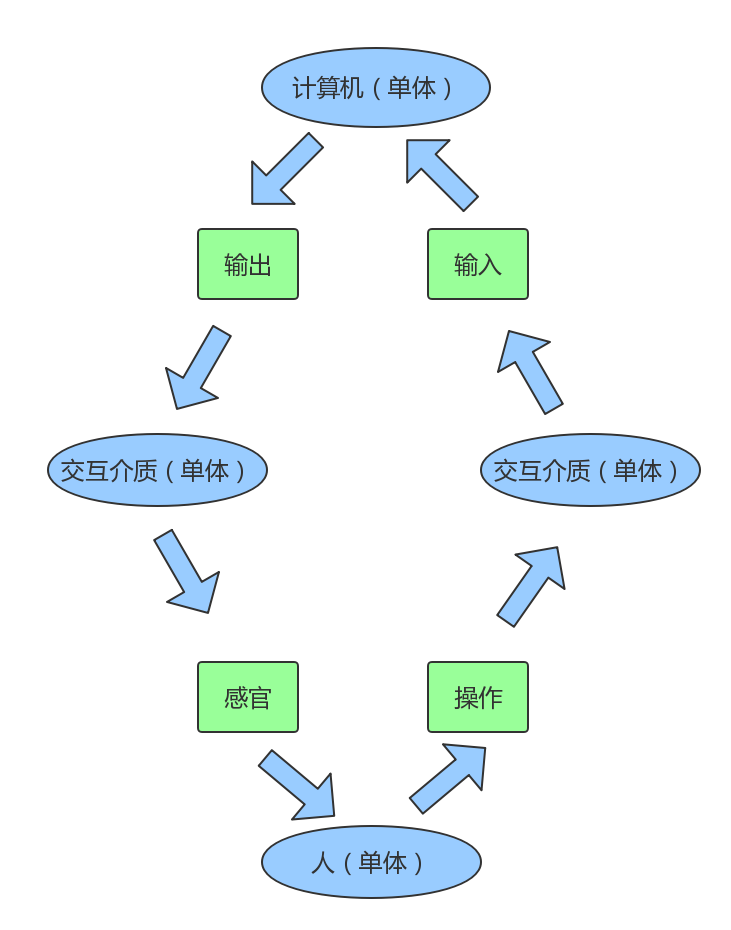
也就是说,群体 = 单体 + ... + 单体这条公式是正确的,我们可以将群体直接视为多个单体的简单相加。
# 流
虽然我们知道,所有的事物(包括交互介质)都可抽象为一个个的单体,但一个个单体之间是怎么衔接起来呢?
我们将所有的输入和输出抽象为“流”,对于流的传递(交互),我们使用熟悉的事件监听的方式:
function 监听器(输入流, 单体) {
输入流.变更 = 输入流 => {
单体(输入流);
};
}
而我们单体的输出流,通常也是其他单体的输入流,于是我们能看到整个流的流动:
单体n输出 = 单体n(...单体2(单体1(输入)));
如果说我们需要流式处理我们的流,使用典型的 jQuery 链式调用方式,我们可以在创建单体的时候添加对于单体方法:
function 添加流处理(...n个单体){
// 注册流的链用方法
n个单体.forEach((单体, n) => {
流.单体n = function() {
this = 单体(this);
return this;
}
})
}
单体1 = 单体();
...
单体n = 单体();
添加流处理(单体1, ..., 单体n);
此时我们将流调整为第一人称,则有比上面稍微优雅的方式:
输出流 = 输入流.单体1().单体2().[...].单体n();
# 光与电的世界
我们来将抽象模型实例化。假设我们的世界,驱动能量为光和电,即各个单体的输入输出都只有光和电。 注意,这里我们将光和电视为两种完全独立的能源,可作为流的一种。
# 光和电的单体
上面我们假设,单体和单体之间的交流通过电、光,所以我们得到这样的单体:
function 单体(输入) {
输入光 = 输入.光;
输出光 = 处理光(输入光);
输入电 = 输入.电;
输出电 = 处理电(输出电);
// 输出
return {
光: 输出光,
电: 输出电
};
}
从上面推出群体可抽象为个体,则我们的世界也是一个承接光电流的单体,而它对光和电的处理方式主要表现为传播(减弱或增强):
function 世界(输入) {
输入光 = 输入.光;
输出光 = 传播(输入光);
输入电 = 输入.电;
输出电 = 传播(输出电);
// 输出
return {
光: 输出光,
电: 输出电
};
}
我们假设世界是没有输入的,因此我们需要手动添加能量的来源:
function 创建世界() {
const 输入 = {};
输入.光 = 添加光源();
输入.电 = 添加电源();
return 世界(输入);
}
说白了,我们创建了世界这样一个特殊的单体,同时给世界提供光和电的能量源。
# 光和电的传播机制
从前面调整的流的第一人称链式用法,我们不难得到光和电的传播机制都符合:
输出流 = 输入流.单体1().单体2().[...].单体n();
而流从何处开始输入,又将在何处输出,取决于哪一段是你所需要观察的而已。
我们创建一个世界之后:
- 流的规则设定好,流开始流动;
- 流的流动,表现为各单体对流的 输入 => 处理 => 输出;
- 单体和世界、单体间通过流来进行交互,表现为 输入 => 处理 => 输出;
- 其中每一段流作为研究对象,抽象成单体或者群体进行分析。
当然,这与现实世界中的光和电的传播十分相似:
- 对不同物质会产生不同的效果(单体的处理)。
- 会在经过不同的物质之后,增强或是减弱(输入流和输出流)。
# 结束语
以上尽是一些遐想,如果说太过于抽象,其实把流换成我们熟悉的程序中的数据流,或许容易理解得多。
假设我们代码之中,一切可作为流,DOM 的事件流、http 请求流,然后通过各种函数(单体)来驱使我们的流流动,也不妨为一种有趣的角度。
